(footnote: here lies Quantum Mechanical Spin)
This post continues the discussion of how ferromagnets work as considered in part 1, part 2 and part 3. The previous parts dealt with the basics of electromagnetism, introducing the connections from Maxwell’s equations to the magnetic field, illustrating the origin of the magnetic dipole and finally demonstrating how force is exerted on a magnetic dipole by a magnetic field.
In this post, I will extend in a totally different direction. All of the previous work was highlighting magnetism as it occurs with electromagnets, how electric currents create magnetic field and respond to those fields. The magnetic dipoles I’ve outlined to this point of time are loops of wire carrying electric current. Bar magnets have no actual electrical wires in them and do not possess any batteries or circuitry, so the magnetic field coming from them must be generated by some other means. The source of this is a cryptic phenomenon that is in its nature quantum mechanical. I did hint at it in part 3, but I will address it now head on.
In 1922, Walther Gerlach and Otto Stern published an academic paper where they brought to light a weird new phenomenon which nobody had seen prior (it’s actually the third paper in a series that describes the development of the experiment, with the first appearing in 1921). That paper may be found here if you aren’t stuck behind a pay wall. Granted, the paper is in German and will require you to find some means of translation, but that is the original paper. The paper containing the full hypothesis is here.
In their experiment Stern and Gerlach built an evaporator furnace to volatilize silver. Under a low pressure vacuum, as good as could be attained at the time, silver atomized from the furnace was piped through a series of slits to collimate a beam of flying silver atoms. This beam of silver atoms was then passed through the core of a magnetic field generated by an electromagnet in a situation much as mentioned previously in the context of Lorentz force.
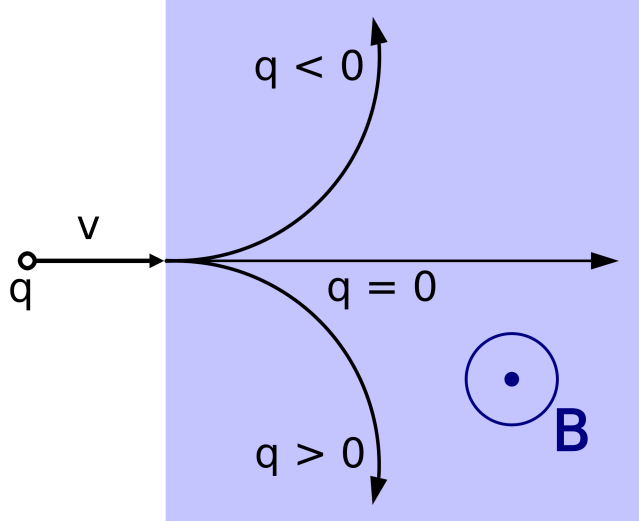
As illustrated here, one would expect a flying positive charge ‘q’ with velocity ‘v’ to bend one way upon entering magnetic field ‘B’, while a negative charge bends the other. Without charge, there is no deflection due to Lorentz force. In the Stern-Gerlach experiment, the silver atom beam passing through the magnetic field then impinges on a plate of glass, where the atoms are deposited. This glass plate could be taken and subjected to photographic chemistry to “develop” and enhance the intensity of the silver deposited on the surface, enabling the experimenters to see more clearly any deposition on the surface of the glass. According to the paper, the atom beam was cast through the magnetic field for 8 hours in a stretch before the glass plate was developed to see the outcome.
The special thing about the magnetic field in the Stern Gerlach experiment is that, unlike the one in the figure above, it was intended to have inhomogeneity… that is, to be very non-uniform.
For the classical expectations, a silver atom is a silver atom is a silver atom, where all such atoms are identical to one another. From the evaporated source, the atoms are expected to have no charge and would be undeflected by a magnetic field due to conventional Lorentz force, as depicted above. So, what was the Stern-Gerlach experiment looking for?
Given the new quantum theory that was emerging at the time, Stern and Gerlach set out to examine quantization of angular momentum of a single atom. Silver is an interesting case because it has a full d-orbital, but only a half-filled s-orbital. In retrospect, s-orbitals are special because they have no orbital angular momentum themselves. This in addition to the other closed shells in the atom would suggest no orbital angular momentum for this atom. In 1922, the de Broglie matter wave was not yet proposed and Schrodinger and Heisenberg had not yet produced their mathematics; quantum mechanics was still “the old quantum” involving ideas like the Bohr atom. In the Bohr atom, electron orbits are allowed to have angular momentum because they explicitly ‘go’ around, exactly like the current loop that was used for calculations in the previous parts of this series. The idea then was to look for quantized angular momentum by trying to detect magnetic dipole moments. A detection would be exactly as detailed in part 3 of this series; magnetic moments are attracted or repelled depending on their orientation with respect to an external magnetic field.
In their experiment, Stern and Gerlach did what scientists do: they exposed a glass plate to the silver beam with the electromagnet turned off, and then they turned around and did the same experiment with the magnet turned on. It produced the following set of figures:

The first circle, seen at left, is Figure 2 from the paper, where there is no magnetic field exerted on the beam. The second circle, with the ruler in it, is Figure 3, where a magnetic field has now been turned on. In the region at the center or the image, the atom beam is clearly split into two bands relative to the control exposure. The section of field in the middle of the image contains a deliberate gradient, where the field points horizontally with respect to the image and changes strength going from left to right. One population of silver diverts left under the influence of the magnetic field while a second population diverts right.
Why do they deviate?
What this observation means is that the S-orbital electron in an evaporated silver atom, having no magnetic dipole moment due to the orbital angular momentum of going around the silver atom nucleus, has an intrinsic dipole moment in and of itself that can feel force under the influence of an external magnetic field gradient. This is very special.
The figure above is an example of a quantum mechanical “observation” where what has appeared is “eigenstates.” As I’ve repeated many times, when you make an observation in quantum mechanics, you only ever actually see eigenstates. In this case, it is a very special eigenstate with no fully classical analog, Spin. For fundamental spin, especially the spin of a silver atom with a single unpaired S-orbital, there are only two possible spin states, called now spin-up and spin-down. Spin appears by providing a magnetic dipole moment to a “spinning” quantum mechanical object. The electron, having a charge and a spin, has a magnetic dipole moment and is therefore responsive to magnetic field gradient. The population of silver atoms passing into the magnetic field deflect relative to this tiny electron dipole moment, where the nucleus is being dragged by the “S-orbital” electron state due to the electrostatic interaction between the electrons and the nucleus. The dipole moment is repelled or attracted in the magnetic field gradient exactly as described in part 3, and since this dipole is quantum mechanical, it samples only two possible states: oriented with the external field or oriented against it, giving two bands in the figure above.
The conventional depiction of the magnetic dipole formed by a wire loop can be adopted to the quantum mechanical phenomenon of spin by adding a scale adjustment called the gyromagnetic ratio. This number enables the angular momentum actually associated with the spin quantum number to be scaled slightly to account for the strength of the magnetic dipole produced by that spin. This is necessary since a particle carrying a spin is not actually a wire loop –the great peculiarity of spin is that if it is postulated as the internal rotation of a given particle, the calculated distribution of the object in question tends to break relativity in order to generate the appropriate angular momentum, leading most physicists to consider spin to be a quantum mechanical phenomenon that is not actually the object ‘spinning’. For all intents and purposes, spin is very like actual rotational spin and it shows up in a way that is very similar to electric charges running around a wire loop.
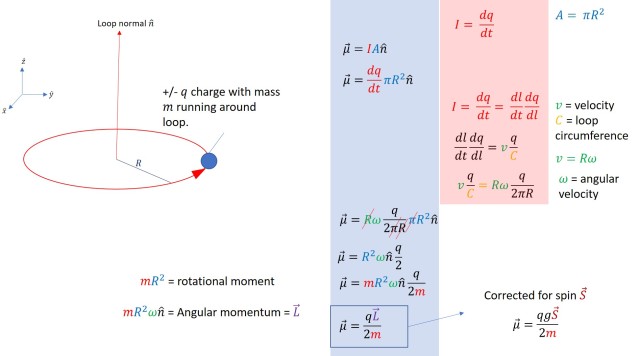
The math in this figure is quick and fairly painless; it converts magnetic dipole moment from a wire loop into a magnetic dipole moment that is due to spin angular momentum. The equation at the start is classical. The equation at the end is quantum mechanical. One thing that you often see in non-relativistic quantum mechanics is that classical quantities adopt into quantum mechanics as operators, so the thing at the very end is the magnetic dipole moment operator. This quantity can be recast various ways, including with the Bohr magneton and in various adjustments of g while the full operator is useful in Zeeman splitting and in NMR.
The existence of spin gives us a very interesting quantity; this is a magnetic dipole moment that is intrinsic to matter in the same way as electric charge. It simply exists. You don’t have to create it, as in the wire loop electromagnet, because it is already just there. There is no requirement for batteries or wires. Spin is one candidate source for the magnetic dipole moment that is required to produce a bar magnet.
It is completely possible to attribute the magnetism of bar magnets to spin, but saying it this way is actually something of a cop-out. How are atoms organized so that the spin present in atoms of iron becomes large enough to create a field that can cause a piece of metal to literally jump out of your hand and go sliding across the table? Individual electronic and atomic spins are really very tiny and getting them to organize in such a way that many of them can reinforce each other’s strengths is difficult. I’ve said previously that chemistry is wholly dependent on angular momentum closures and one will note that atomic orbitals fill or chemically bond in such a way as to negate angular momentum: for example, S-orbitals (and each and every available orbital) are filled by two electrons, one spin-up and one spin-down, so that no individual orbital is left with angular momentum. Sigma bonds and Pi bonds are formed so that unpaired electrons in any atom may be shared out to other atoms in order for participants to cancel their spin angular momentum. While there are exceptions, like radicals, nature generally abhors exposed spin. Even silver, the atoms of which are understood to have detectable spin, is not ferromagnetic: you can’t make a bar magnet out of silver! What conspires to make it possible for spin to become macroscopically big in bar magnets? This is the one big puzzle left unanswered.
As an interesting aside, in their paper, Stern and Gerlach add an acknowledgement thanking a “Mr. A. Einstein” for helping provide them with the electromagnet used in their experiment from the academic center he headed at the time.
The final post in this series can be found at Part 5: Orienting Magnetization.
