Magnets, how do they work? (part 2)

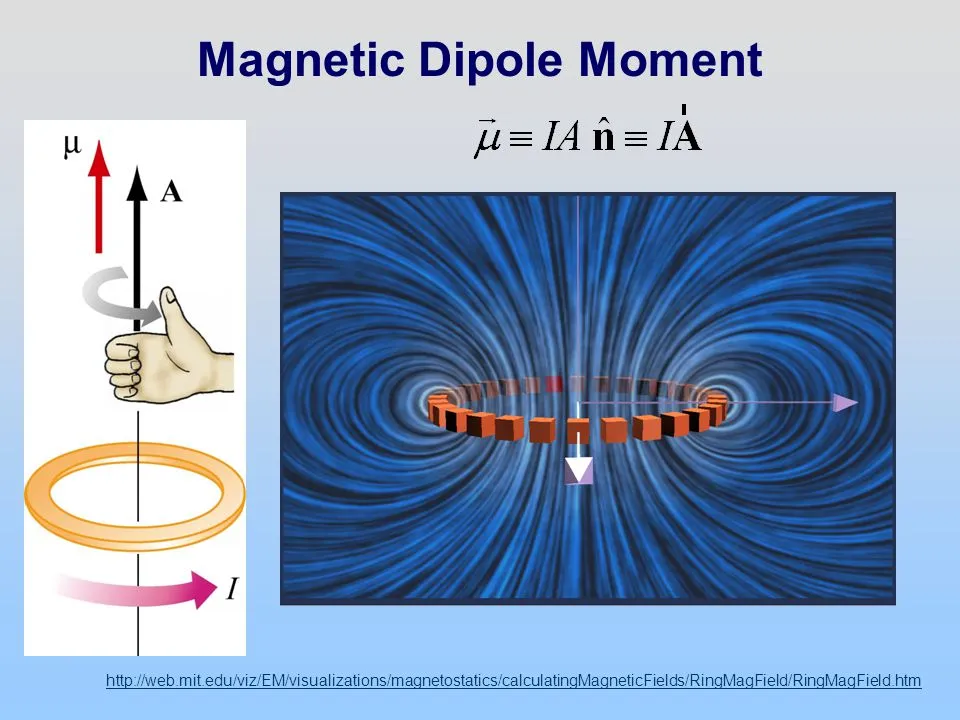
(Previous post: Part 1: Magnetic field) I will talk about the origin of the magnetic dipole construct here. Consider a loop of wire… You may have noticed that I posted an entry entitled “NMR and Spin flipping (part 2)” which has since disappeared. It turns out that wordpress doesn’t synch so well between its mobile …