(Warning: spoilers about "The Creator") I haven't been overly motivated to write in a long time, but maybe saying a little about this will break the dam. If you don't like movie spoilers, beware. I will speak about the newish Gareth Edwards movie "The Creator." I have to say something because this movie has an …
I stand with Ukraine (part 2)
The war is months old. Western media is beginning to drift off into its typical doomcrying lala-land. The United States is as divided and divisive as ever. Even covid is no longer a top headline. One could be forgiven for believing that everything is back to business as usual except for that hideous >$5/gallon at …
I stand with Ukraine
I know several Ukrainian physicists. They are fine people! What hurts me most about Real Politick is the deep anger I feel that my country, a strong country, won't do anything truly substantial to help the Ukrainian people in large part because an obsessed little man is holding me hostage against the actions of my …
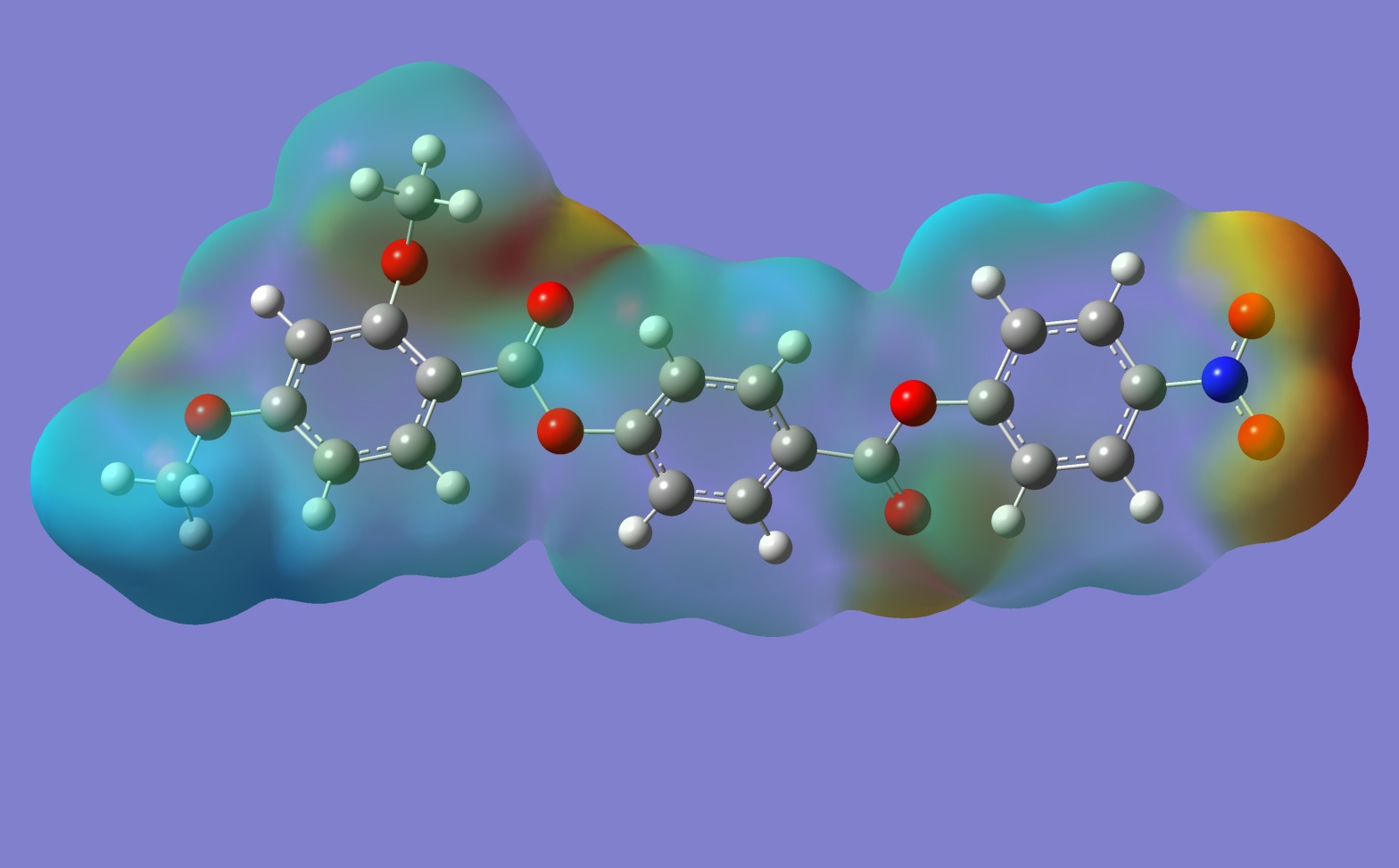
Small Games with Gaussian (6)
The last two years have left me very drained and really not in much of a state to want to post anything on line. Not a whole lot lost, I suppose. I keep telling myself I'll find time to do it, but you really have to make time if you mean it. So, here I …
Small Games with Gaussian (5)
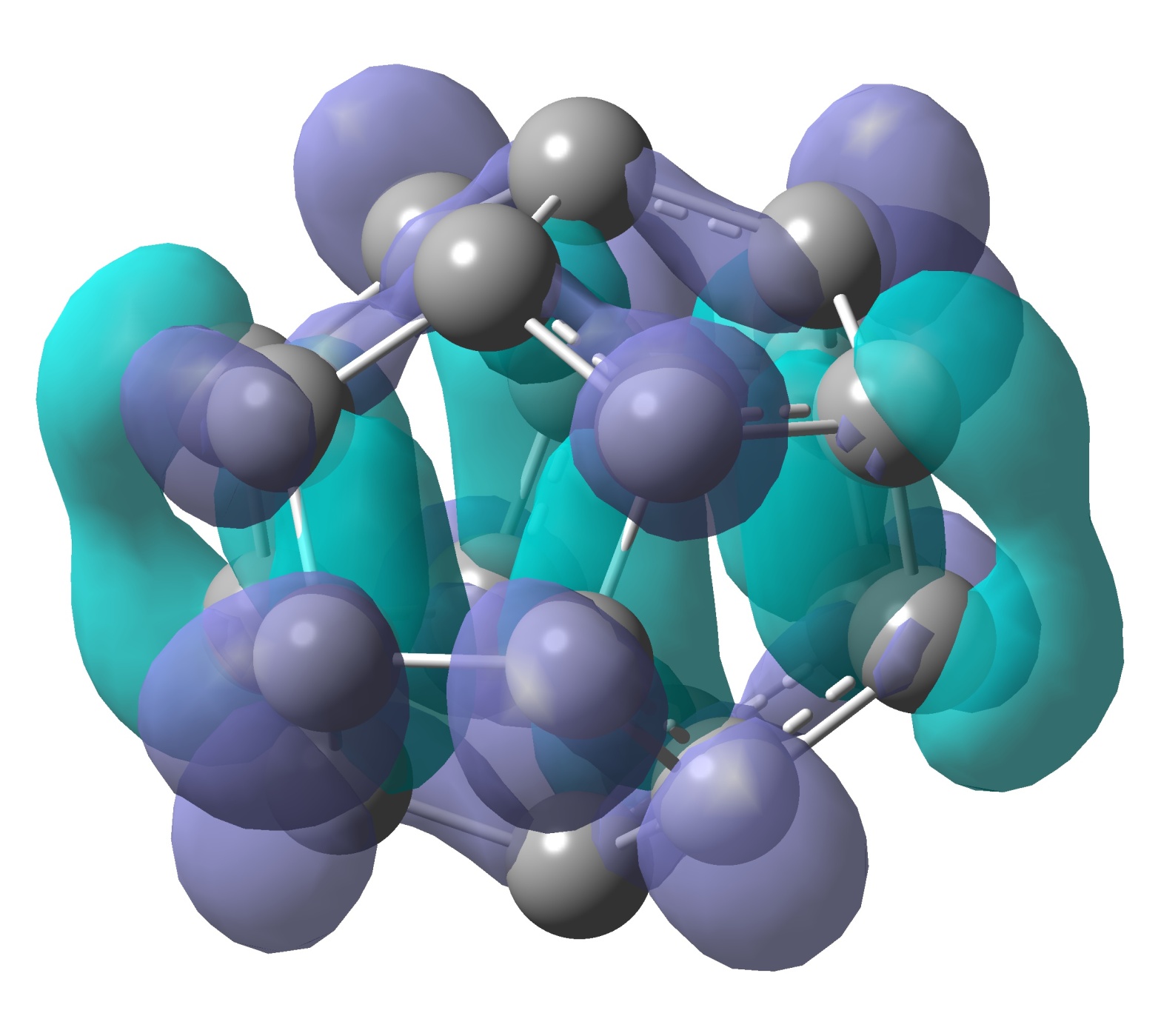
Quick analysis of Carbon-60 (Buckyball) to obtain pretty pictures.
Small Games with Gaussian (4)
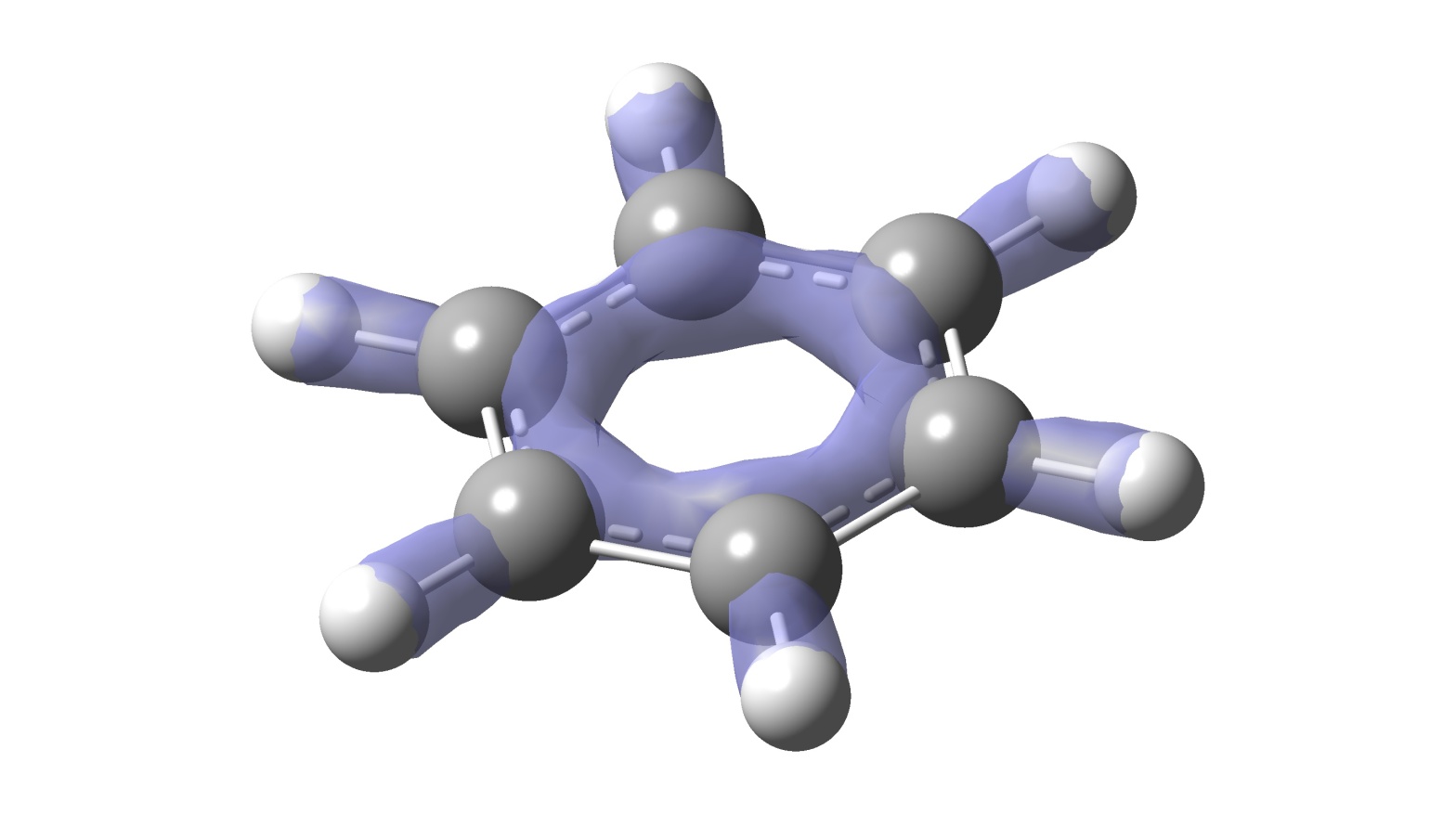
Further games with Quantum Chemistry using Gaussian 16. I bet you never thought anybody would care to write so much about benzene during their free time...
Magnets, how do they work? (part 5)
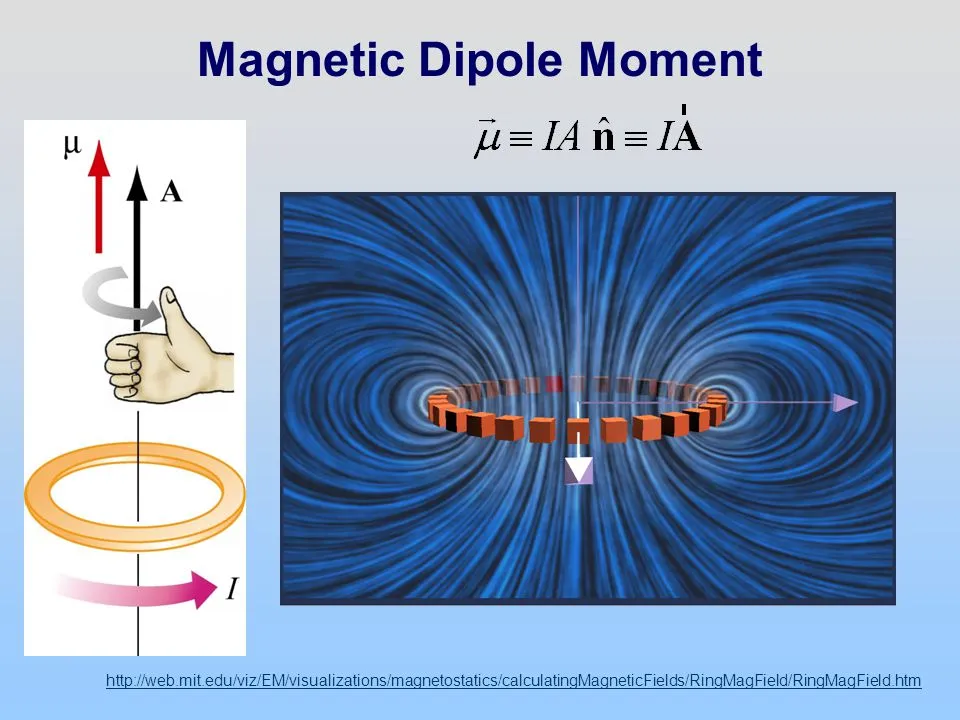
(The last piece to the puzzle. Previous sections can by found here: Part 1: Magnetic Field, Part 2: Magnetic Dipoles, Part 3: Magnetic Force, Part 4: Quantum Mechanical Spin) This post has been sitting on the back burner for a very long time now. I established the physical theory for what a magnetic field is …
Small Games with Gaussian (3)
(Irony that my intro background picture is from GAMESS since I don't have any cool Gaussian pictures to show at the moment.) Okay, you've got an optimized structure for a chemical by an ab initio method. You just spent months learning Hartree-Fock, then Density Functional Theory and even dabbled a bit in the nether regions …
Small Games with Gaussian (2)
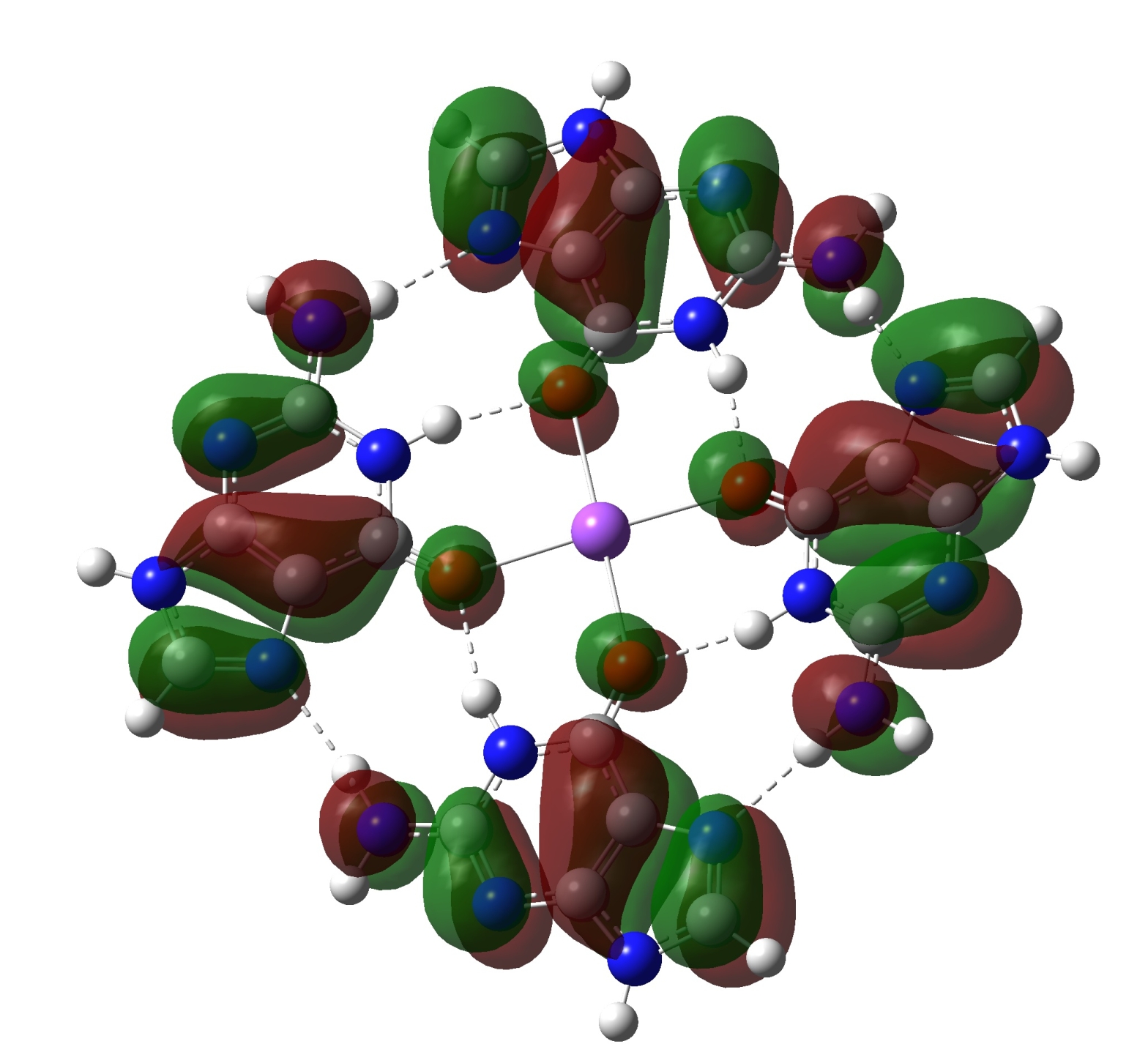
Subtitle: Return of the G-quartet This post will mainly just be pretty pictures. As I've been working with Gaussian, I've found that some of my earlier work with GAMESS wasn't holding up. I took the time to go back and see if a couple of my earlier efforts with the G-quartet were still valid, or …
Small Games with Gaussian (1)
I don't have a huge amount of time to talk about it at the moment, but something kind of cool has happened. This is a small extension off my quantum chemistry series. For much of the last year, I've been putting huge amounts of time into ab initio calculation using the General Atomic and Molecular …